WHAT IS QUANTITATIVE DATA?

Quantitative data is data in the form of numbers.

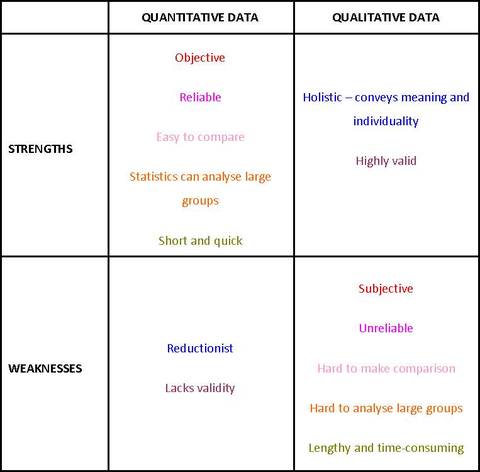
This includes number scores, rankings, tally marks, percentages, statistical measures and various types of graphs.

You could remember that quaNtitative involves Numbers whereas quaLitative involve Letters.

The main advantage of quantitative data for psychologists is that it is objective - numbers mean the same thing to everyone and you don't need to interpret them personally; this makes quantitative data very reliable and highly scientific.

Another advantage is that quantitative data is good for making comparisons. This is particularly important for the experimental method, which involves comparing the DV for different conditions of the IV. Quantitative data can be turned into statistics, which allows detailed comparisons of large groups and the identification of trends.

Finally, quantitative data is simple. Numbers can summarise data very quickly and with little space whereas descriptions in words may be very lengthy or time-consuming. This applies to collecting the data in the first place as well as studying it later.

The main drawback with quantitative data is that it is reductionist. This means it simplifies too much. A lot of detail and meaning is lost when human experience is presented quantitatively. Two participants may get the same scores, even if they got those scpores by doing very different things.

• For example, two respondents could fill out a questionnaire completely differently but get the same overall score
• In an observation, tallying the number of times a behaviour took place gives researchers a frequency score but it doesn't tell you what the behaviour was like (serious or playful? successful or unsuccessful? enthusiastic or half-hearted?) or why the person acted as they did

Because of this, quantitative data may lack validity: it may not tell you what you want to know and it can even be quite misleading. For a lot of people, quantitative data tells them nothing at all!

If you compare the strengths and weaknesses of quantitative data to those of qualitative data, you will see they are opposites:

ANALYSING QUANTITATIVE DATA

You learned most of what you need to know about analysing quantitative data at primary school or the early years of secondary school.

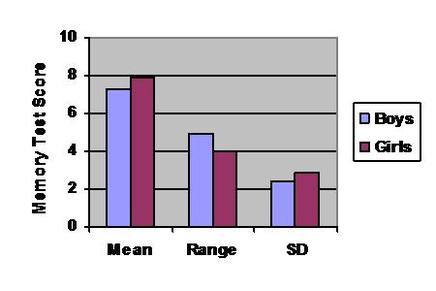
Descriptive statistics are the straightforward calculations that analyse a sample of numbers. You should recognise the mean, the mode and the median; standard deviation might be a bit more obscure. These, and the graphs based on them, are explained below. Inferential statistics, which use a data sample to draw conclusions about the wider population it was taken from, are a bit more complicated and are discussed elsewhere.

MEASURES OF CENTRAL TENDENCY

There are three simple statistics you already know: the mean, the median and the mode.

The mean is the average of a set of scores. You calculate it by adding the scores together and dividing by the number of scores in the set.

• A mean can be a number that doesn't exist in the set and this can cause it to make no sense. For example, the average family has 1.9 children, but how can you be 0.9 of a child?
  
• Means are easily "skewed" by extreme high or extreme low scores called "outliers". For example, the average wage in the country is yanked up by a few billionaires who are staggeringly rich. If there are outliers, the mean may lack validity.
  

The mode is the most frequent score in the set, the one that occurs the most often. It's useful for showing the most popular or common result.

• Unlike the mean, the mode is always an actual score from the set. For example, the mode is for British families to have 1 child; it's the most common family size.
  
• Unlike the mean, there could be more than one mode if several different score "tie" for popularity. This can be confusing.
  
• The mode helps us interpret the mean; if mode and mean are similar, it suggests there is standard distribution of data, but if they are far apart it suggests the data is skewed
  

The median is the central score, the one(s) in the middle when the scores are all ranked in order, highest to lowest. If there is an even number of scores, then the median is the average of the two middle ones.

• The median may or may not be an actual number from the set, depending on whether the set has an odd number of scores and an actual middle number.
  
• Unlike the mean, the median is not skewed by outliers
  

MEASURES OF DISPERSION

These are slightly more complex statistics, but the simplest is something you already know: the range. The other is standard deviation.

The range is the difference between two ends of a set of scores. You work it out by taking the highest score and deducting the lowest one.

• As with the mean, the range is skewed (stretched, in this case) by outliers
• A large range suggests the scores are dispersed but a small range suggests they are "bunched" around the mean
  

Standard deviation is a bit more complex.

Standard deviation is a more sophisticated way of looking at the mean. If you arranged everybody's scores in a line, you'd expect them to "bunch up" around the mean and "thin out" as you get further away from the mean. That's usually what happens.

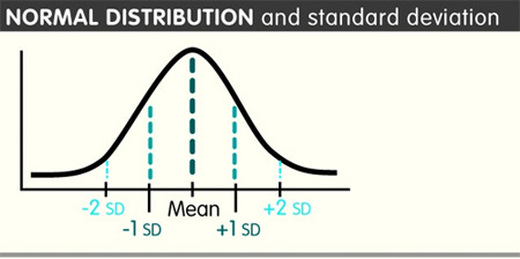
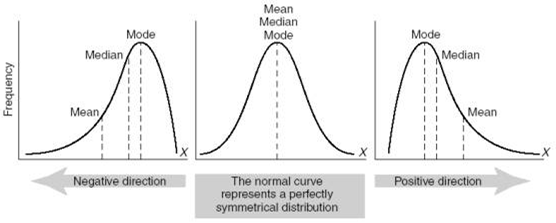
If you did this as a graph, it would be a curve that looked like a bell - a "bell curve". The "lump" at the top of the bell is where most of the scores bunch up, the flat ends to the left and the right are where the less common scores spread out. This pattern is also known as standard deviation.

So if the mean is the lump in the middle, there are a bunch of scores that are pretty close to the mean to the left and the right.

All the scores up to 34% lower or 34% higher than the mean - that's 68% of the set in total - are one Standard Deviation (1 SD) away from the mean. Being within 1 SD makes your score pretty "normal" statistically speaking.

Another 14% (so, 35-48%) are higher and lower than that: we're talking 96% of all the scores who fall within 2 SD of the mean. Being within 2 SD makes you "unusual".

Then there are the people who fall outside the 96%, the ones in the bottom 2% and the top 2%. These scores are 3+ SD away from the mean and count as "very unusual" (or just plain "weird").

You can calculate standard deviation by following these steps:

• Calculate the mean
• Deduct the mean from each score in your set
• Square each result (multiply it by itself)
• Add the squared results together
• Divide by n-1 (the number of scores in your set, minus 1)
• The result is your variance; the standard deviation (SD) is the square root of your variance

Alternatively, lots of websites will quickly calculate SD for you

Calculate standard deviation here

Standard deviation is a relatively quick (!) way of telling if any particular score from your set is normal - if it's within ±1 SD of the mean.

However, this only works if you have standard distribution (clue: the mean and mode are very similar):

If the mean is a lot lower than the mode, you probably have negatively skewed data; if it's much higher, you have positively skewed data.

Standard deviation is not helpful with a skewed distribution of data.

CALCULATING FREQUENCIES

Often, your data is a set of scores, but sometimes it is a set of tallies or frequencies instead. This is known as nominal level data.

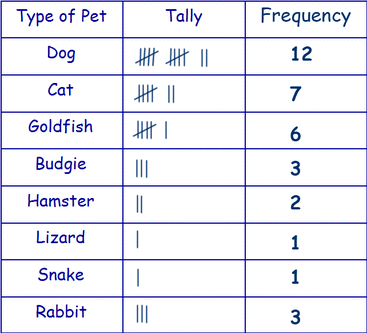
You might collect the data as tallies. For example, you could count the different types of pets classmates have.

You can't work out a mean from this level of data, but the mode is very useful (dog is the most common pet).

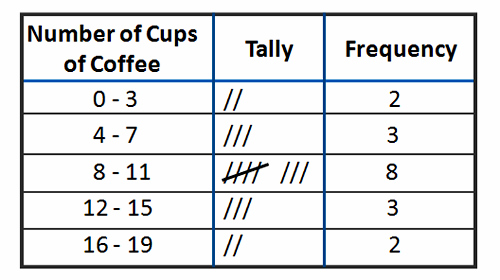
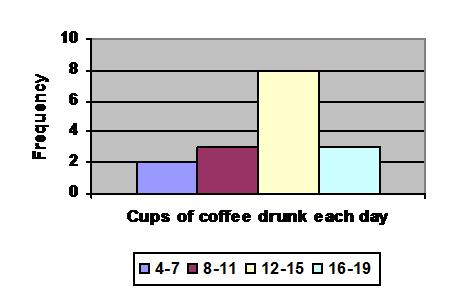
You could also collect the data as scores (known as interval/ratio level data) and then turn them into frequencies by putting the scores into categories. For example, you could find out how many cups of coffee other students drink each day and turn that into frequencies.

Notice that it's up to you how to group the frequencies. If you grouped the coffee as 0-7, 8-15 and 16+ you would have fewer categories but much bigger frequencies (5, 11 and 2)

You can turn frequecies into percentages quite easily:

• Add up the total number of tallies
• To work out any given frequency as a percentage, divide it by the total number of tallies, then multiply it by 100
  

GRAPHICAL REPRESENTATION OF DATA

When you carry out research, you end up with "raw data", which is each participant's scres or a table of tallies. It's tempting to make a pretty graph out of this.

DON'T DO IT.

No one wants to look at a graph of raw data. Why would they? They could get the same information off the scores themselves and it would be less confusing.

Graphs should interpret the data. They should help you see patterns in it that you would miss if you looked at the raw data.

There are lots of graphs to choose from, but only two are mentioned in the Specification: bar charts and histograms.

BAR CHARTS

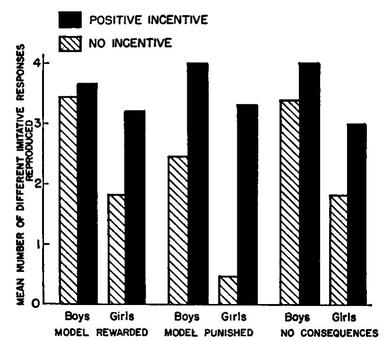
Your measures of central tendency and dispersion can be turned into a bar chart.

A few rules for bar charts:

• The X axis (up the left side) MUST be labelled to tell us what the numbers mean
• The bars must be coded so we know what they stand for
  
• The bars don't touch if they stand for different things

HISTOGRAMS

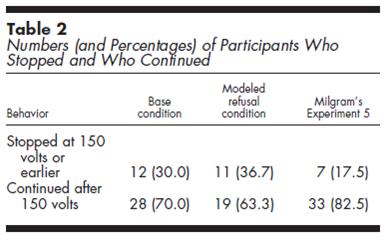
Frequencies can be turned into histograms.

A few rules for histograms:

• The X axis (up the left side) must be labelled "Frequency"
• The bars must be coded so we know what groupings of tallies they stand for
• The bars must touch
  
• There must be a blank space where the frequency is 0

APPLYING QUANTITATIVE DATA IN PSYCHOLOGY
AO2

Most of the studies in this course make use of quantitative data, so you will usually be criticising them for a lack of qualitative data. For example, although Milgram includes a few descriptions of his participants groaning and shaking, he doesn't quote their responses during debriefing or question them about what they thought or felt during the study.

There are some studies that include both types of data: Watson & Rayner's study of Little Albert includes detailed quantitative data about Albert's behaviour on different dates, but also film footage of Albert which counts as qualitative data. Bandura also filmed his 1963 study.

There are a few studies that might benefit from more quantitative data. Sherif's Robbers Cave study gathered some basic quantitative scores for how the boys rated each other as friends and what they thought of the other group, but it's mostly qualitative descriptions of the boys' behaviour from Sherif's perspective and this lacks objectivity.

If you look at some of the original studies in the Resources section of the site, you'll see how the psychologists presented their graphical data. For example, Schmolck et al. (2002) use bar charts like this:

This shows the participants' mean number of correct responses to yes/no questions for living and non-living images. CON is the healthy control group, HF is the MTL group (minus H.M.) and MTL+ is the more severely brain damaged patients. Actual scores are shown as dots; H.M.'s scores are shown as squares (so this is adding raw data to the table in an unobstrusive way). Notice that the two sets of bars don't touch because they refer to different data sets.

Bandura (1965) uses a similar bar chart to show means:

This is a good bar chart: the bars from different sets of data don't touch, the X-axis is labelled and the bars are clearly coded. Bandura doesn't show raw data as dots:  there were 11 boys and 11 girls in each condition so that would have cluttered the graph, but it would have been helpful to see the outliers to get a sense of the dispersal of the scores.

Burger (2009) doesn't use graphs at all. Instead he shows tables of data:

Was Burger right to show the frequencies and percentages as numbers on a table or would a graph have made this clearer?

EXEMPLAR ESSAY
How to write a 8-mark answer

Evaluate the use of quantitative data in Psychology. (8 marks)

• A 8-mark “evaluate” question awards 4 marks for describing the use of quantitative data (AO1) and 4 marks for evaluating it (AO3). You need a conclusion to get a mark in the top band (7-8 marks). "Quantitative data" turns up in the Specification for the Social and Cognitive Approaches but you need to know how data is used in all the Approaches.
  

Description
Quantitative data is information in number form. This includes tables and graphs.
One type of quantitative data is measures of central tendency. This includes means, modes and medians.
You calculate the mean by adding all the scores in a set together and dividing the total by the number of scores in the set.
You can represent this sort of information in a bar chart which could show the means for two conditions of the IV side-by-side.

Application
The strength of quantitative data is that it is objective. This is because numbers mean the same thing to everybody so no personal bias comes into interpreting them.
Quantitative data can also be used to make comparisons and, if it is converted into statistics, whole groups can be analysed.
However. quantitative data is reductionist. It only shows a superficial layer to human behaviour and doesn't explore meaning.
It can also be misleading. For example, two people could get the same quantitative score in completely different ways (eg answering questions completely differently).

Conclusion
Quantitative data helps research be more scientific because you can replicate quantitative research and see if you get the same results. This is an advantage over qualitative research which is much more personal.

• Notice that for a 8-mark answer you don’t have to include everything about quantitative data. I haven’t mentioned standard deviation or frequencies or the difference between bar charts and histograms. But it is a balanced answer - half description, half application.